Fits a symmetric Gaussian model to visibility amplitude data for validation purposes. More...

#include "data_visibility_amplitude.h"
#include "model_symmetric_gaussian.h"
#include "model_ensemble_averaged_scattered_image.h"
#include "likelihood.h"
#include "sampler_affine_invariant_tempered_MCMC.h"
#include "utils.h"
#include <mpi.h>
#include <memory>
#include <string>

Include dependency graph for symmetric_gaussian_comparison.cpp:

Functions
int	main (int argc, char *argv[])

Detailed Description

Author: Avery Broderick

Date: June 2017

Compares a symmetric Gaussian model to the visibility amplitude data taken in 2007 and 2009, permitting a day-specific intensity renormalization. The primary fit result is a measure of the size of the emission region and can be compared to the fit results reported in Broderick et al. (2011) (see, especially, Fig. 4). The resulting parameter distribution is:

Triangle plot showing the likely parameter values and associated confidence contours. A burn in of 10 MCMC steps was assumed (corresponding to the first 1280 values).

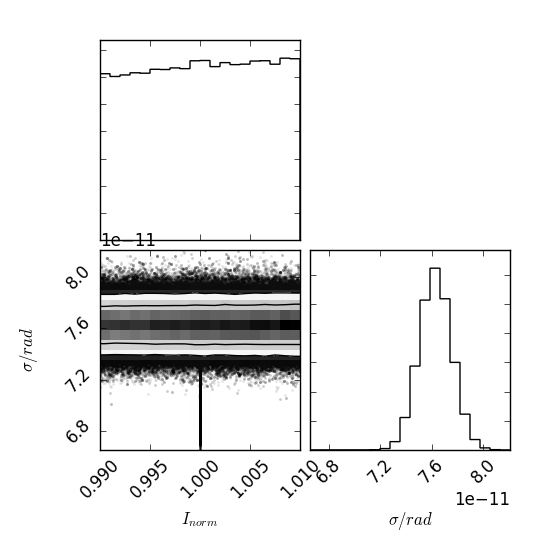
Note that the intensity normalization is solved for analytically in the likelihood_marginalized_visibility_amplitude, and thus the intrinsic normalization is fixed near unity by design. The size (std. dev.) of the Gaussian, \(\sigma\), is given in radians; \(7.6\times10^{-11}~{\rm rad}=15.7~\mu{\rm as}\), and thus the recovered probability distribution quantitatively matches the best fit size in Broderick et al. (2011), \(\sigma=15.8\pm0.2~\mu{\rm as}\) very well.

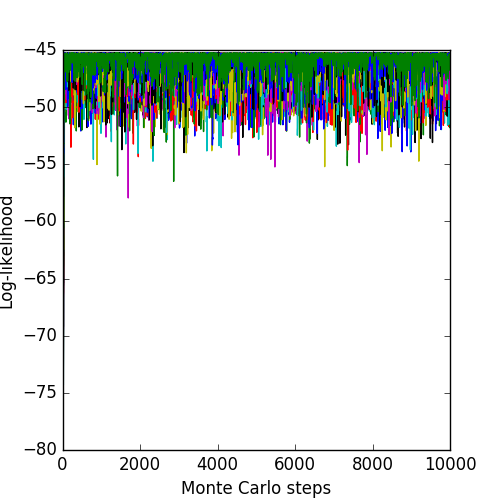
The parameter values associated with the individual chains may also be plotted:

Trace plot showing the fluctuations in the parameters for each MCMC chain as a function of MCMC step.

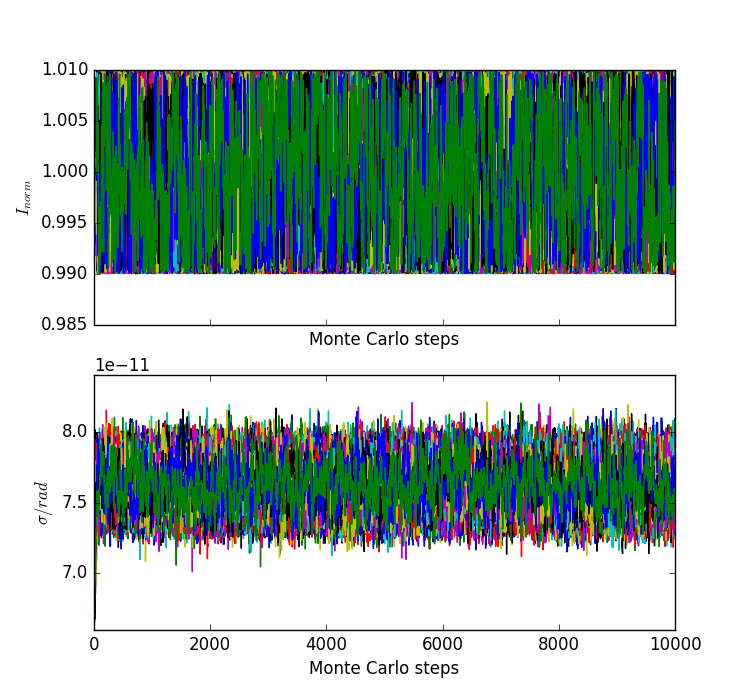
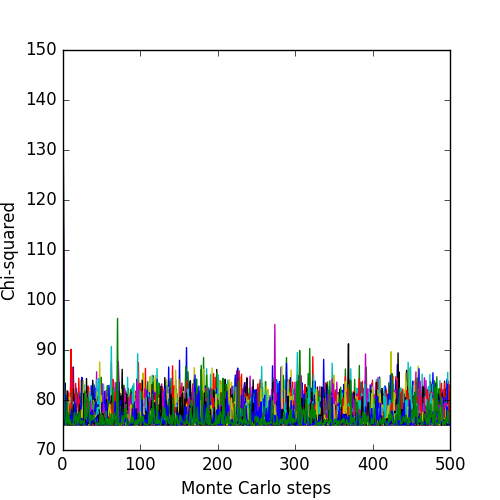
Again, the intensity normalization is pinned near unity. The size of the Gaussain rapidly finds the minimum and the probability distribution of steps converges. The associated log-likelihoods and \(\chi^2\) of the chains are:

Log-likelihoods of the individual chains as a function of MCMC step.

Chi-squared of the individual chains, outputted every 20 MCMC steps (note that the coordinate shows the same range in steps as the previous plot, despite its misnomer).

Functions

Detailed Description