Samples an extremely muti-modal and spiky likelihood surface in five dimentions. More...
#include "likelihood.h"#include "sampler_affine_invariant_tempered_MCMC.h"#include "sampler_differential_evolution_tempered_MCMC.h"#include <mpi.h>#include <memory>#include <string>
Functions | |
| int | main (int argc, char *argv[]) |
Detailed Description
- Date
- Feb 2020
Testing the ability of the sampler to sample multi-modal likelihood distributions. This main file samples a five dimensional egg-box likelihood with 3125 modes. The natural logarithm of the likelihood is given by:
\(\log{(L(\mathbf{x}))} = -2.0 * (2.0 + \prod_{n=1}^{5} cos(x_i))^{5} \)
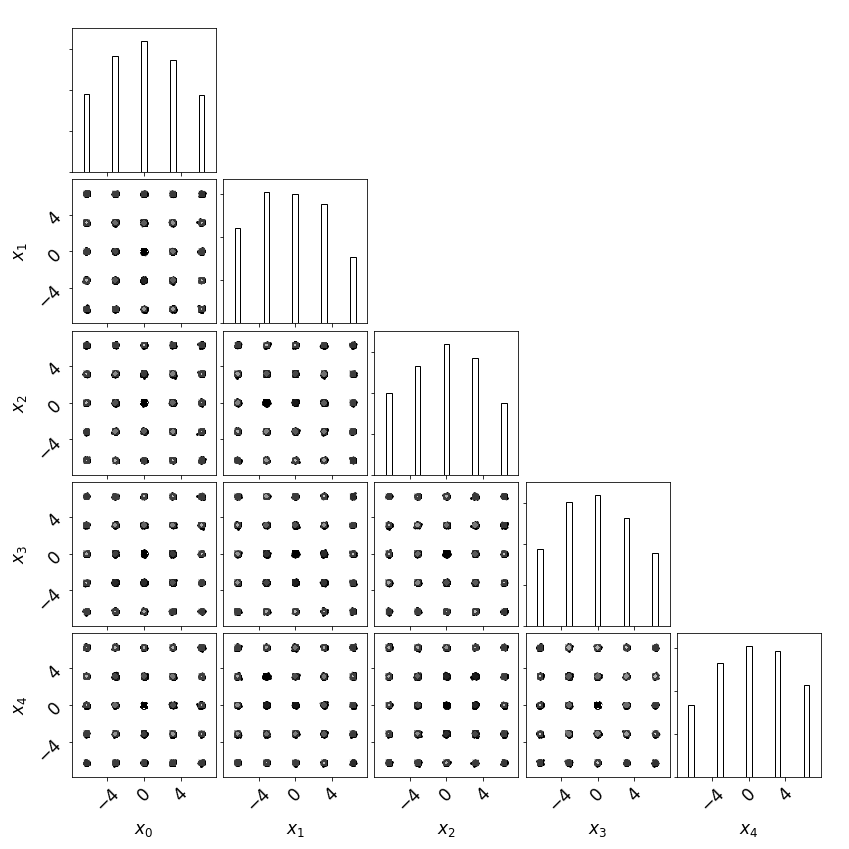
Using the output chain file the marginalized distributions are calculated and plotted:
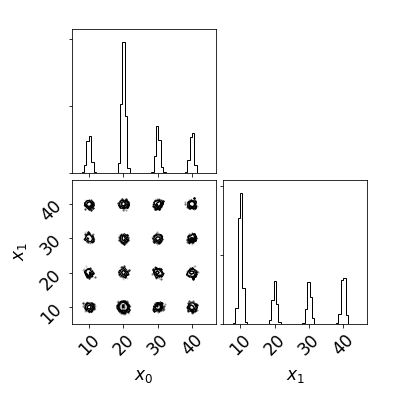
Additionally we used a likelihood composed of 16 well-separated gaussians in two dimensions to show we can recover the relative heigth of the peaks. All the gaussians were the same except for one with the likelihood nine times as large. Here is the triangle plot showing the likelihood distribution:
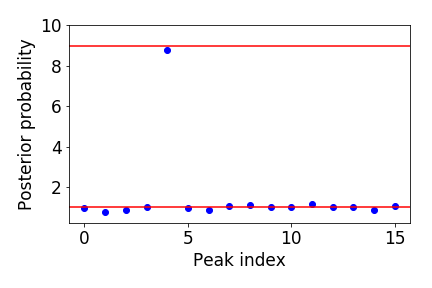
The following plot shows the integrated probability successfully recovered for each gaussian peak using the output MCMC chain file. As can be seen all the peaks are identical except for one that is nine times taller.
- Date
- June 2017
Testing the ability of the sampler to sample multi-modal likelihood distributions. This main file samples a five dimensional egg-box likelihood with 3125 modes. The natural logarithm of the likelihood is given by:
\(\log{(L(\mathbf{x}))} = -2.0 * (2.0 + \prod_{n=1}^{5} cos(x_i))^{5} \)
Using the output chain file the marginalized distributions are calculated and plotted:

Additionally we used a likelihood composed of 16 well-separated gaussians in two dimensions to show we can recover the relative heigth of the peaks. All the gaussians were the same except for one with the likelihood nine times as large. Here is the triangle plot showing the likelihood distribution:

The following plot shows the integrated probability successfully recovered for each gaussian peak using the output MCMC chain file. As can be seen all the peaks are identical except for one that is nine times taller.


